The Bekenstein Bound:
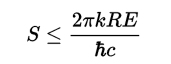
Not to be confused with Broadway Bound.
At any rate, I came across this equation in a book I’m reading on physics. Here’s what Wikipedia says:
In physics, the Bekenstein bound is an upper limit on the entropy S, or information I, that can be contained within a given finite region of space which has a finite amount of energy—or conversely, the maximum amount of information required to perfectly describe a given physical system down to the quantum level. It implies that the information of a physical system, or the information necessary to perfectly describe that system, must be finite if the region of space and the energy is finite. In computer science, this implies that there is a maximum information-processing rate (Bremermann’s limit) for a physical system that has a finite size and energy, and that a Turing machine with finite physical dimensions and unbounded memory is not physically possible.
The universal form of the bound was originally found by Jacob Bekenstein as the inequality where S is the entropy, k is Boltzmann’s constant, R is the radius of a sphere that can enclose the given system, E is the total mass–energy including any rest masses,
To put it more succinctly in a way that I can understand (that is, language that encourages me to eat doughnuts), The maximum amount of information that can be contained increases with mass. Mass/Energy. Whatever.
More doughnuts for me. I must increase gain weight to get smarter.




 I bought this book on the last day of the local GAME Expo in October. You’ll have to take my word for it, as I did not post a picture of the things I bought on that trip. I bought it from the author, who traipsed all the way from Boston to sit at a table in Springfield, Missouri, to sell her books. I was her last sale of the day, as she was heading out to catch a plane home as we got to the game / science fiction convention on Sunday afternoon.
I bought this book on the last day of the local GAME Expo in October. You’ll have to take my word for it, as I did not post a picture of the things I bought on that trip. I bought it from the author, who traipsed all the way from Boston to sit at a table in Springfield, Missouri, to sell her books. I was her last sale of the day, as she was heading out to catch a plane home as we got to the game / science fiction convention on Sunday afternoon.
 The title of this book certainly fits into the philsophy kinds of books that I might like to pick up. Its size (short and paperback) meant it would make a good carry book for me. It did. As I was reading it at the dojo, a very well-read teenager there recognized Watts’ name. After I finished it, I saw a Facebook image with a Watts quote on it. So his influence continues, some thirty-five years after his death.
The title of this book certainly fits into the philsophy kinds of books that I might like to pick up. Its size (short and paperback) meant it would make a good carry book for me. It did. As I was reading it at the dojo, a very well-read teenager there recognized Watts’ name. After I finished it, I saw a Facebook image with a Watts quote on it. So his influence continues, some thirty-five years after his death.




 Technically, the copy of this book that I read is the third book in a three-novel omnibus edition called 3 Martian Novels; however, the other two are Thuvia, Maid of Mars and The Chessmen of Mars, both of which I read earlier this year when I read the omnibus
Technically, the copy of this book that I read is the third book in a three-novel omnibus edition called 3 Martian Novels; however, the other two are Thuvia, Maid of Mars and The Chessmen of Mars, both of which I read earlier this year when I read the omnibus 

 This book represents my annual Christmas book, and it’s the one I bought most recently (
This book represents my annual Christmas book, and it’s the one I bought most recently (




 It’s been almost six months since I’ve read a Bolan book (
It’s been almost six months since I’ve read a Bolan book (